LAMP: Extracting Text from Gradients with Language Model Priors
Dimitar I. Dimitrov
November 28, 2022
Data privacy and Federated learning
Machine learning algorithms have set the state-of-the-art on most tasks where large amount of training data is available. While the improvements brought by these algorithms are impressive, their applications to settings where private data is used remain limited due to the privacy concerns posed by the large centralized datasets required by the training procedures. Recently, the federated learning framework has emerged as a promising alternative to collecting and training with centralized datasets. In federated learning, multiple data owners (clients) collaboratively optimize a loss function $l$ w.r.t. the parameters $\theta$ of a global model $h$ on their own dataset $\mathcal{D}_i$ without sharing the data in $\mathcal{D}_i$ with the other participants:
\[\begin{equation*} \min_{\theta} \frac{1}{n} \sum_{i=1}^n \mathbb{E}_{(x, y) \sim \mathcal{D}_i} \left[ l(h_\theta(x), y) \right]. \end{equation*}\]To this end, the optimization is carried out in communication rounds. In particular, given the global parameters $\theta_t$ at round $t$, multiple clients compute model updates $g$ on their own data and then share them with a central server that aggregates them and produces a new global parameters $\theta_{t+1}$. After several communication rounds the model parameters converge to an optimum.
One common implementation of this generic framework is the FedSGD algorithm, where updates are given by the gradient of $l$ w.r.t. $\theta_t$ on a single batch $\{(x^b_i, y^b_i)\}\sim \mathcal{D}_i$ of client data of size $B$:
Federated learning in theory allows for improved data privacy, as the client data does not leave the individual clients. Unfortunately, several recent works have shown that updates $g$ computed by common federated algorithms such as FedSGD can be used by a malicious server during the aggregation phase to approximately reconstruct the client’s data. So far, prior work has focused on exposing this issue in the image domain where strong image priors help the reconstruction. In this work, we show that such approximate reconstruction is also possible in the text domain, where federated learning is very commonly applied.
Gradient leakage
In order to obtain approximate input reconstructions $\{\tilde{x}^b_i\}$ from the FedSGD update of some client $i$, with updates as described above, prior works typically solve the following optimization problem at some communication round $t$:
\[\begin{equation} \min_{\\{\tilde{x}^b_i\\}} \sum_{i=1}^n \mathcal{L}_{rec}\left( \left(\frac{1}{B} \sum_{b=1}^B \nabla_\theta l(h_\theta(\tilde{x}^b_i), y^b_i)\right), g(\theta_t, \mathcal{D}_i) \right) + \alpha_{rec}\,R(\{\tilde{x}^b_i\}), \end{equation}\]where $\mathcal{L}$rec is distance metric - e.g., $L_1$, $L_2$ or cosine, that measures the gradient reconstruction error, $R(\{\tilde{x}^b_i\})$ is some domain specific prior - e.g. Total Variation (TV) in the image domain, that assesses the quality of the reconstructed inputs, and $\alpha_{rec}$ is hyperparameter balancing between the two. Note that $\theta_t$ and $g(\theta_t, \mathcal{D}_i)$ are known by the malicious server as the former is computed by it and the latter is sent to it by client $i$ at the end of the round. Often the batch labels $\{y^b_i\}$ can be obtained by the server using specific label reconstruction attacks, that are beyond the scope of this blog post, or just guessed by running the reconstruction with all possible labels due to their discrete nature, so throughout the post we only focus on reconstructing $\{\tilde{x}^b_i\}$. In our previous blog post, we have shown that solving the optimization problem above is equivalent to finding the Bayesian optimal adversary in this setting.
In the image domain, the optimization problem is typically solved using gradient descent on the batch of randomly initialized images $\{x^b_i\}$ using an image-specific prior $R$. In the next section, we first discuss why such a solution is not well suited to language data and we then discuss our method, LAMP, that combines a text-specific prior with a new way to solve the optimization problem above by alternating discrete and continuous optimization steps to obtain our state-of-the-art gradient leakage framework for text.
LAMP: Gradient leakage for text
In this work, we focus our attention on transformer-based models $h_\theta$, as they are the state-of-the-art for modeling text across various language tasks. As these models operate on continuous vectors, typically they assume fixed-size vocabulary of size $V$ and embed each word into a different $\mathbb{R}^d$ vector. For a sequence of words of size $n$, we refer to the individual words in it with $t_1,\ldots,t_n$ and to their corresponding embeddings with $x_1,\ldots,x_n$.
In order to solve the gradient leakage optimization problem from the previous section, we choose to optimize directly over the embeddings $x_i$ as they, similarly to images, are represented by continuous values we can optimize over. However, uniquely to the text domain, only a finite subset of vectors in $\mathbb{R}^d$ are valid word embeddings. To this end, when we obtain our reconstructed embeddings $\tilde{x}_i$ for each of them we then select the most similar in cosine similarity token in the vocabulary to create a reconstruction of the sequence of words $\tilde{t}_1,\ldots,\tilde{t}_n$.
An additional issue that is specific to the text domain and, in particular, the transformer architecture is that the transformer outputs depend on word order only through positional embeddings. Therefore, the model gradient reconstruction loss $\mathcal{L}$rec is not as affected by wrongly reconstructed word order as it is by the wrongly reconstructed word embeddings themselves. In practice, this results into the continuous optimization process often getting stuck in local minima caused by an embedding of a token that reconstructs the correct word at the wrong position. These local minima are hard to escape from continuously. To this end, we introduce a discrete optimization step that reorders the sentence periodically, allowing to escape the local minima. The discrete step works by first proposing several word order changes such as swapping the positions of two words or moving a sentence prefix to the end of the sentence. The different order changes are then assessed based on the combination of the gradient reconstruction $\mathcal{L}$rec and the perplexity of the sentence $\mathcal{L}$lm computed by auxiliary language model such as GPT-2 on the projected words $\tilde{t}_i$:
\[\begin{equation} \mathcal{L}_{rec}(\{\tilde{x}_i\}) + \alpha_{lm}\,\mathcal{L}_{rec}(\{\tilde{t}_i\}), \end{equation}\]where $\alpha_{lm}$ is a hyperparameter balancing the two parts. The resulting end-to-end alternating optimization is demonstrated in the image below:
where green boxes show the discrete optimization steps and the blue boxes demonstrate the continuous gradient descent optimization steps of the gradient leakage objective presented in the previous section.
Finally, similarly to the image domain, we introduce a new prior specific to text that improves our reconstruction. To this end, we made the empirical observation that during optimization often the embedding vectors $x_i$ grow in length even when their direction doesn’t change a lot. To this end, we regularize the average vector length of the embeddings in a sequence $\tilde{x}_i$ to be close to the average embedding length in the vocabulary $l_e$:
\[\begin{equation} R(\tilde{x}_i) = \left(\frac{1}{n}\sum_{i=1}^n \| \tilde{x}_i \|_2 - l_e\right)^2 \end{equation}\]This allows our embeddings to remain in the correct range of values, which in turn results in a more stable and accurate reconstruction of the embeddings $\tilde{x}_i$.
Experimental evaluation
We evaluated LAMP on several standard sentiment classification datasets and architectures based on the BERT language models. As is typically the case with language models, we assume our models are pretrained to make word predictions on large text corpora and that federated learning is used only to fine-tune the models on the classification task at hand. We consider two versions of LAMP - one where $\mathcal{L}$rec is a weighted sum of L1 and L2 distances (denoted LAMPL1+L2), and another one where $\mathcal{L}$rec is the cosine similarity (denoted LAMPcos). We compare them to the state-of-the-art attacks - TAG based on the same L1+L2 distance, and DLG based on L2 distance alone. We evaluate the methods in terms of the Rouge-1 metric (R1) which measures the percentage of correctly reconstructed words and the Rouge-2 metric (R2) which measures the percentage of correctly reconstructed bigrams. We note one can interpret R2 as a proxy measurement of how well the order of the sentence has been reconstructed. We present a subset of the results shown in our paper on the CoLA dataset and batch size of 1 below:
| $\text{TinyBERT}_6$ | $\text{BERT}_{BASE}$ | $\text{BERT}_{LARGE}$ | ||||
|---|---|---|---|---|---|---|
| Method | R1 | R2 | R1 | R2 | R1 | R2 |
| DLG | 37.7 | 3.0 | 59.3 | 7.7 | 82.7 | 10.5 |
| TAG | 43.9 | 3.8 | 78.9 | 10.2 | 82.9 | 14.6 |
| $\text{LAMP}_{\cos}$ | 93.9 | 59.3 | 89.6 | 51.9 | 92.0 | 56.0 |
| $\text{LAMP}_{\text{L1}+\text{L2}}$ | 94.5 | 52.1 | 87.5 | 47.5 | 91.2 | 47.8 |
We see that LAMPcos is consistently recovering more words compared to the alternatives with LAMPL1+L2 close behind. Further, LAMP recovers substantially better sentence ordering. It is worth noting that the improvement over the baselines for both R1 and R2 is most pronounced on the smallest model $\text{TinyBERT}_6$ where recovery is the hardest. Additionally, we also experimented with recovering text in the setting where the batch size is bigger than 1. We are the first to present results in this setting and we show them below for the CoLA dataset:
| B=1 | B=2 | B=4 | ||||
|---|---|---|---|---|---|---|
| Method | R1 | R2 | R1 | R2 | R1 | R2 |
| DLG | 59.3 | 7.7 | 49.7 | 5.7 | 37.6 | 1.7 |
| TAG | 78.9 | 10.2 | 68.8 | 7.6 | 56.2 | 6.7 |
| $\text{LAMP}_{\cos}$ | 89.6 | 51.9 | 74.4 | 29.5 | 55.2 | 14.5 |
| $\text{LAMP}_{\text{L1}+\text{L2}}$ | 87.5 | 47.5 | 78.0 | 31.4 | 66.2 | 21.8 |
We see that despite the worse quality of reconstruction, even batch size of 4 still leaks a substantial amount of data. Further, we observe that for bigger batch sizes LAMPL1+L2 performs better than LAMPcos. Both LAMP methods, however, substantially improve upon the results of the baselines.
Finally, we show an example sentence reconstruction from LAMP and TAG on multiple datasets below:
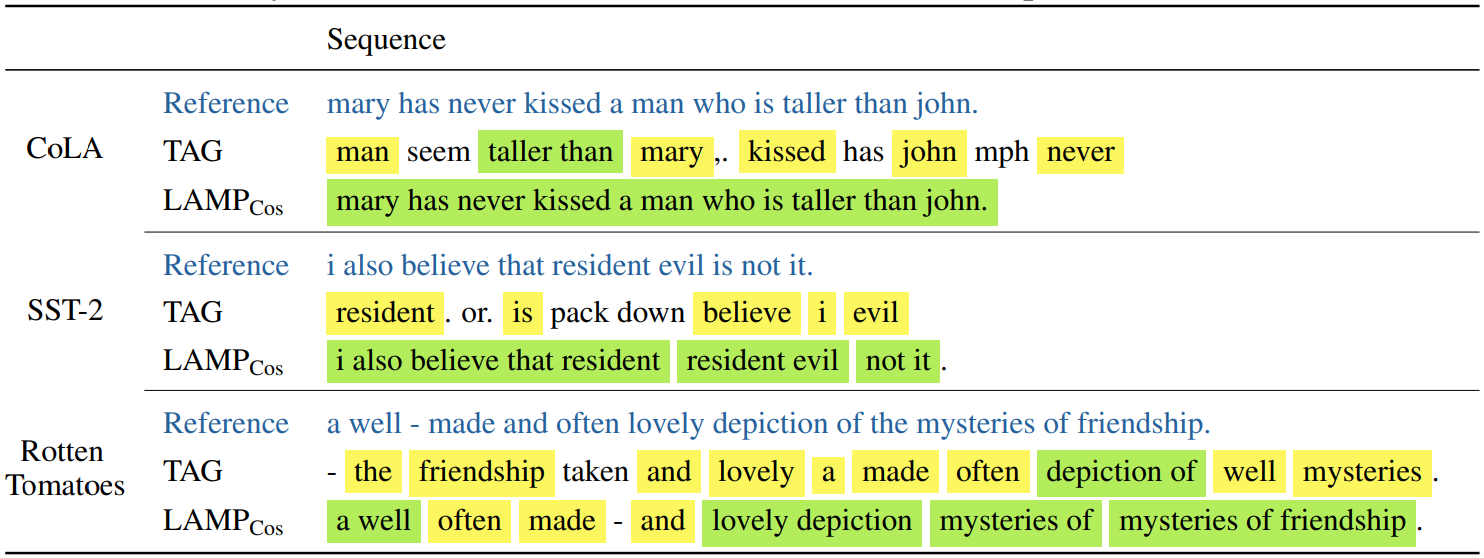 Here, yellow signifies a single correctly reconstructed word and green signifies a tuple of correctly recovered words. We see that LAMP recovers the word order drastically better and often is even able to reconstruct it perfectly. In addition, LAMP recovers more individual words. This confirms qualitatively the effectiveness of our attack.
Here, yellow signifies a single correctly reconstructed word and green signifies a tuple of correctly recovered words. We see that LAMP recovers the word order drastically better and often is even able to reconstruct it perfectly. In addition, LAMP recovers more individual words. This confirms qualitatively the effectiveness of our attack.
Summary
In this blog post, we introduced LAMP, a new framework for gradient leakage of text data from gradient updates in federated learning. Our key ideas are the alternating of continuous and discrete optimization steps and the introduction of an auxiliary text model which we use in the discrete part of our optimization to judge how well a piece of text is reconstructed. Thanks to these elements, our attack is able to produce substantially better text reconstructions compared to the state-of-the-art attacks both quantitatively and qualitatively. We, thus, show that many practical federated learning systems based on text are vulnerable and better mitigation steps should be taken. For more details please see our NeurIPS 2022 paper.

