SynthID-Text is the first publicized large-scale deployment of an LLM watermarking algorithm. It was recently deployed in Gemini App and Web and open-sourced following a Nature publication. While this is a major milestone for watermarking research, the behavior of SynthID-Text in adversarial scenarios remains largely unexplored. In this blog post, we aim to fill this gap by providing a more thorough evaluation, directly leveraging recent work from our group. In the following 4 sections, we investigate if the presence of SynthID-Text can be detected, whether stealing attacks can enable watermark spoofing and removal, and further analyze those spoofing attempts. In each section, we highlight interesting questions that could be explored in future research.
1. The presence of SynthID-Text can be detected
In “Black-Box Detection of Language Model Watermarks” we showed that hiding the fact that an LLM watermark is deployed is not feasible, as watermark presence can be cheaply detected using only black-box queries, for all 3 of the most popular watermarking scheme families.
Extending the results on Gemini 1.0 from the paper, we found no reliable evidence of a watermark on the Gemini 1.5 API.
This matches the official claims, stating that the watermark is only present in the Gemini App and Web.
As those deployments are not suitable for querying with thousands of similar prompts, we ran our tests on a local deployment of a model watermarked with SynthID-Text:
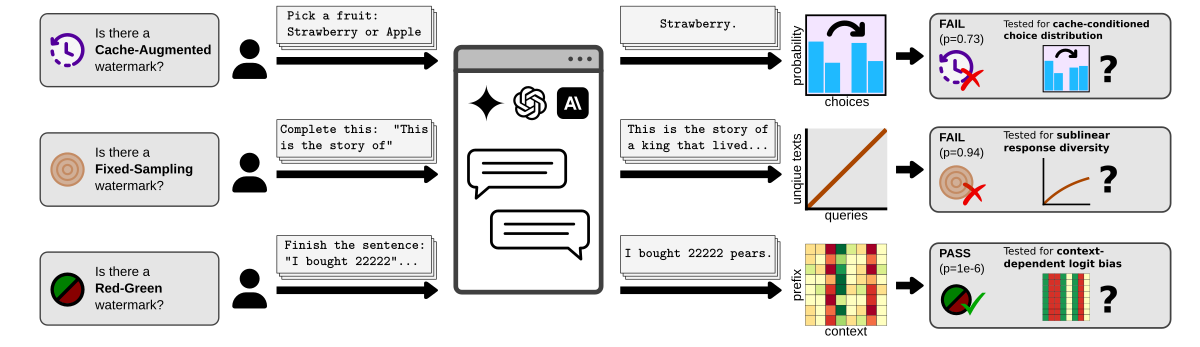 While the first two (as expected) fail, the Red-Green test consistently passes, detecting the watermark presence (\(p \approx 0\)).
This also shows that our tests can be directly applied to newly proposed schemes. To understand why the Red-Green test passes, let’s decompose SynthID into its building blocks as follows:
While the first two (as expected) fail, the Red-Green test consistently passes, detecting the watermark presence (\(p \approx 0\)).
This also shows that our tests can be directly applied to newly proposed schemes. To understand why the Red-Green test passes, let’s decompose SynthID into its building blocks as follows:
SynthID-Text = LeftHash h=3 + Increased context size + Tournament sampling + Caching
From the perspective of a Red-Green scheme, SynthID starts from the LeftHash h=3 variant, increases its context size, and uses tournament sampling to effectively generalize the boosting of green tokens to variable logit biases.
These biases are still consistent for a fixed preceding context, which is the key property our detection test relies on, thus it remains effective.
Next change is caching, i.e., “Repeated context masking” in the original paper.
As in the default SynthID-Text implementation, we set \(K=1\) to achieve single-sequence non-distortion.
Such caching does not fundamentally affect our test, but introduces a new constraint: Instead of upper-bounding, the context size needs to be estimated correctly, as an overestimation would trigger the cache, preventing our queries to extract any information.
Increasing \(K\) would make detection harder, but as discussed in the SynthID-Text supplementary text (G.3), may reduce the watermark effectiveness and increase computational complexity.
Summary: Despite several novel building blocks, the presence of SynthID-Text can be detected in a black-box way using the test for Red-Green schemes, as long as context size estimation succeeds.
Future Work: Can SynthID-Text be tweaked to evade detection (e.g., by increasing \(K\)) without significantly sacrificing its effectiveness? Are viable undetectable schemes possible?
2. SynthID-Text is hard to spoof
In “Watermark Stealing in Large Language Models”, we showed that practical spoofing attacks are possible on SOTA schemes: an attacker can use a set of black-box queries to generate a corpus of watermarked text, and use it to learn to forge the watermark, creating arbitrarily many high-quality watermarked texts. Malicious users could, for instance, generate harmful content and attribute it to the model provider. As spoofing risk was not studied for SynthID-Text, we directly applied our stealing attack to test it, without attempting to optimize the algorithm specifically for this case. Our Spoofing Success metric is FPR*@1e-3: the ratio of spoofing attempts that are both high-quality (rated by GPT4) and fool the watermark detector at a realistic false positive rate of \(10^{-3}\).
Click to see other boring experimental details
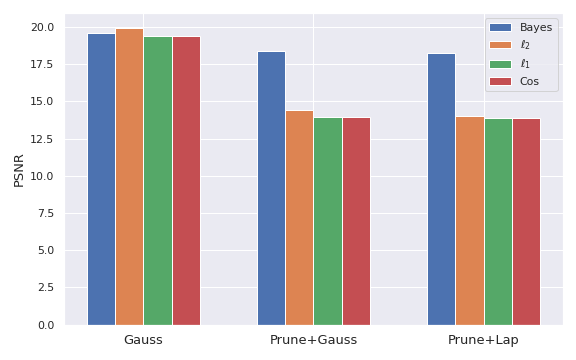
We use Llama2-7B as the watermarked model, and 30k examples from the C4 dataset as black-box queries, using watermarked responses of 800 tokens as the training corpus of our attacker. As the attacker's auxiliary model we use Mistral-7B, and evaluate spoofing on the Dolly-CW dataset. For SynthID-Text we use the default parameters from the paper, with the rigorously controlled FPR, i.e., the weighted mean detector. Average spoofed response is around 450 tokens long. The details of our metric can be found in the original paper.Following the decomposition of SynthID-Text above, we show the results on a range of schemes and variants:
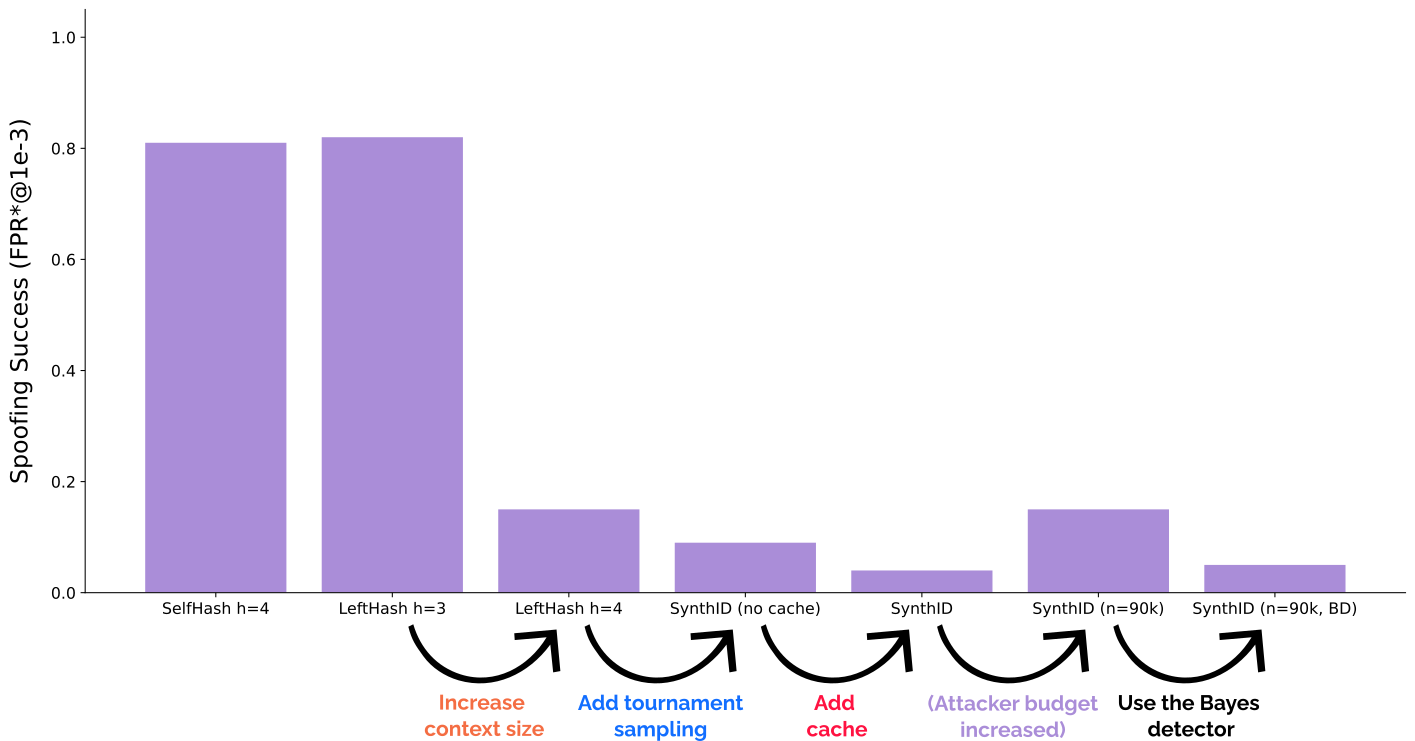
First two bars are copied from our original paper and show that SOTA Red-Green watermarks are highly spoofable with above \(80\%\) success rate. Let’s work towards SynthID-Text. First, increasing the context size of LeftHash greatly reduces spoofing risk, but it still remains non-negligible at \(15\%\). Adding tournament sampling interestingly further reduces this to \(9\%\)—we hypothesize that this comes from our attacker implicitly assuming equal boosting of green tokens, which is no longer the case. We confirm this effectiveness of tournament sampling by directly adding it to LeftHash h=3 and observing a similar drop from \(82\%\) to \(30\%\) spoofing success (not shown in the plot above). Finally, adding caching further drops spoofing success to \(4\%\)! This is caused by the fixed dataset of watermarked text containing less useful signal, as the cache often disables the watermark.
In a simple attempt to improve spoofing success, we tried increasing the number of black-box queries, which indeed helps: tripling the number of queries from \(30k\) to \(90k\) brings spoofing success back to \(15\%\), reversing the effect of the previous two modifications, and suggesting that spoofing may still be possible but much more costly. We finally notice that using the Bayesian detector (BD), despite requiring training data and loosening the statistical guarantee, further helps against spoofing, dropping the success rate to \(5\%\). As the SynthID-Text paper notes, to apply BD to some LLM, it should observe watermarked responses of that LLM, while unwatermarked examples are always taken from the human text distribution. This makes BD effectively a hybrid between a watermark detector and a post-hoc detector, flagging the joint presence of the watermark and the specific LLM. This increases spoofing resistance, as the attacker will use a different model to produce spoofed texts.
Summary: SynthID-Text is harder to spoof compared to other SOTA watermarks, owing this to each of its novel building blocks for different reasons. Increasing the attacker budget may make spoofing viable.
Future Work: Would spoofing be more effective with an order of magnitude larger attacker budget? Can adaptive attacks tailored to SynthID-Text be more successful? Would spoofing via distillation work?
3. Spoofing SynthID-Text via Stealing leaves clues
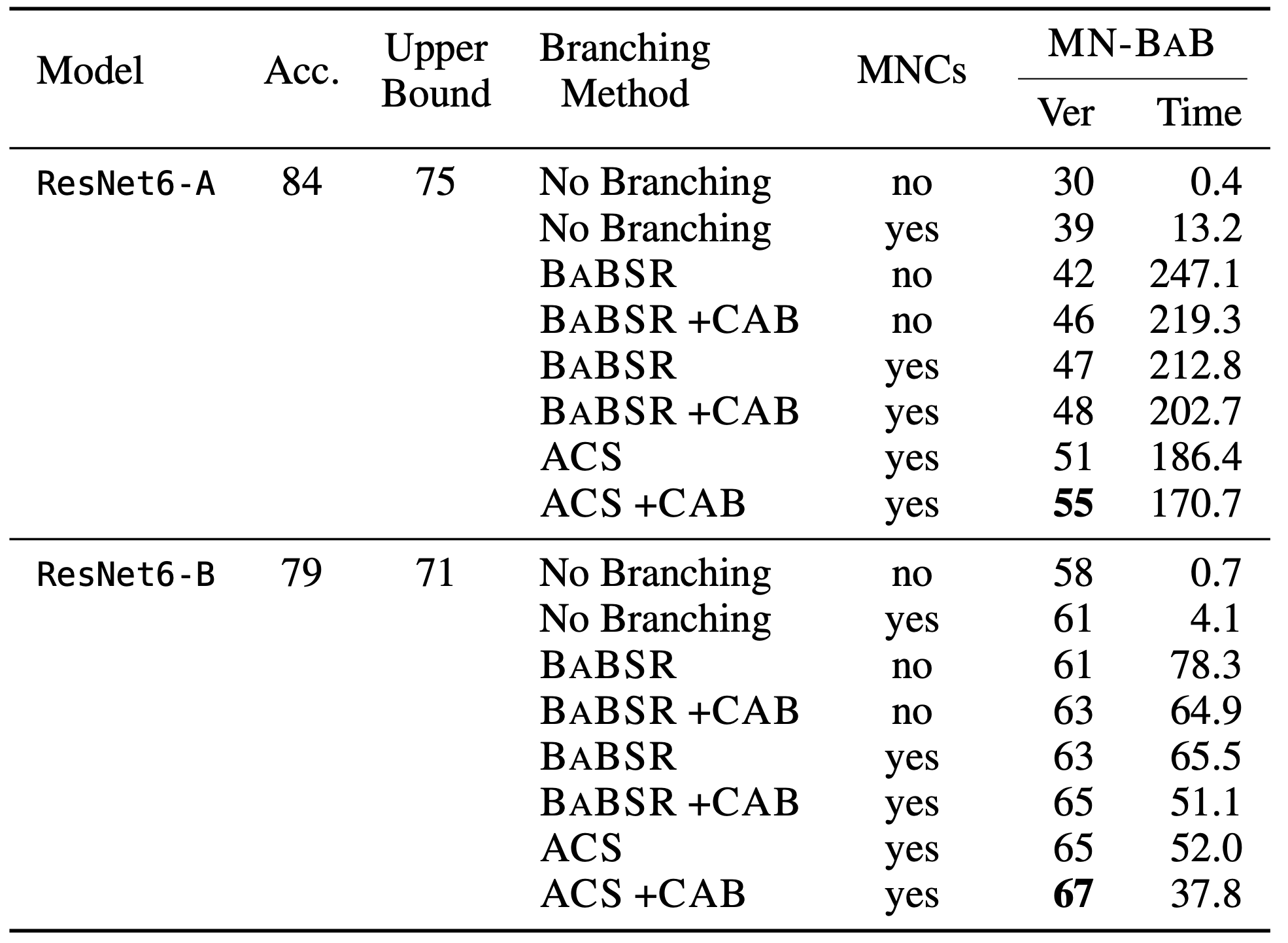
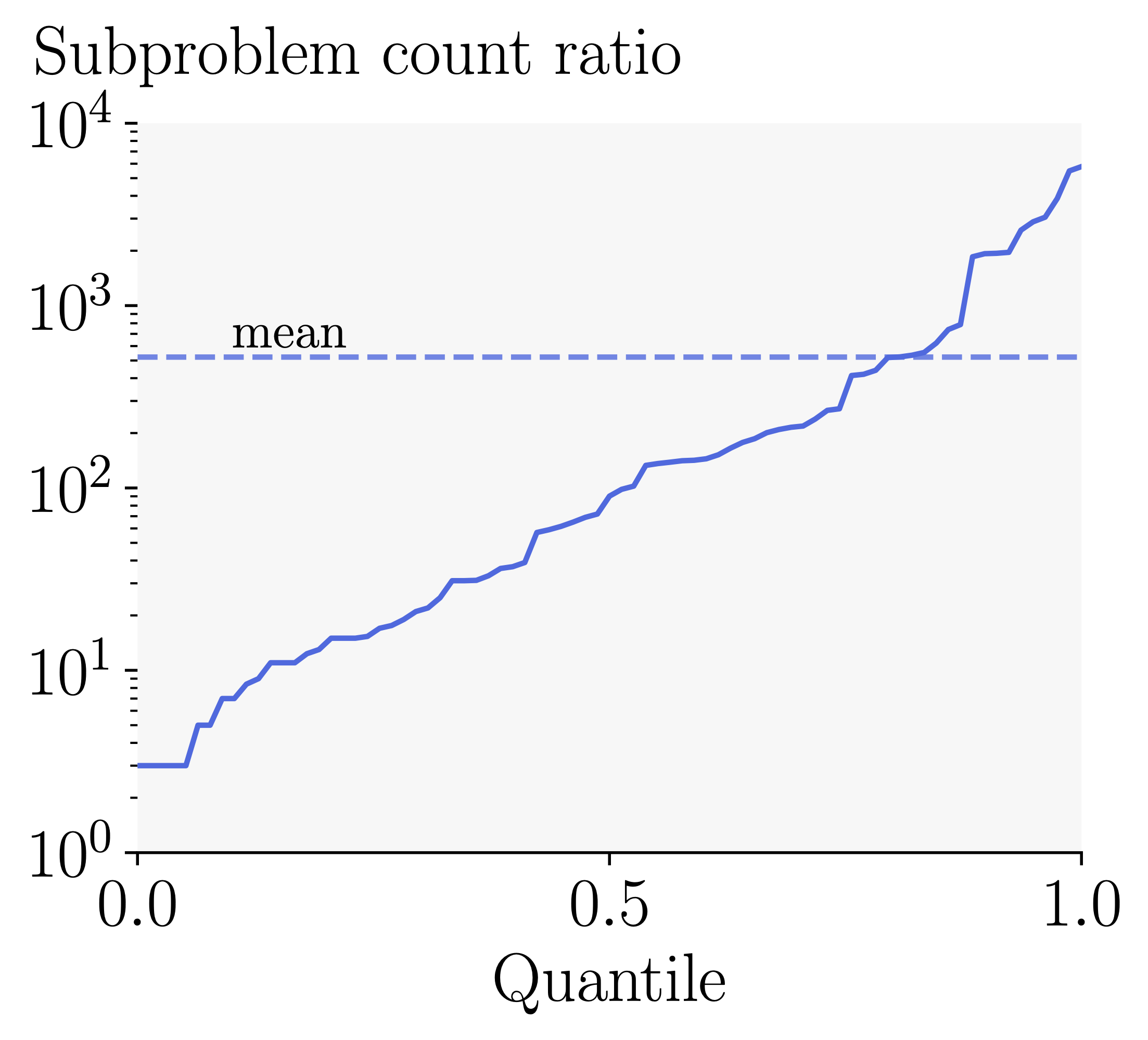
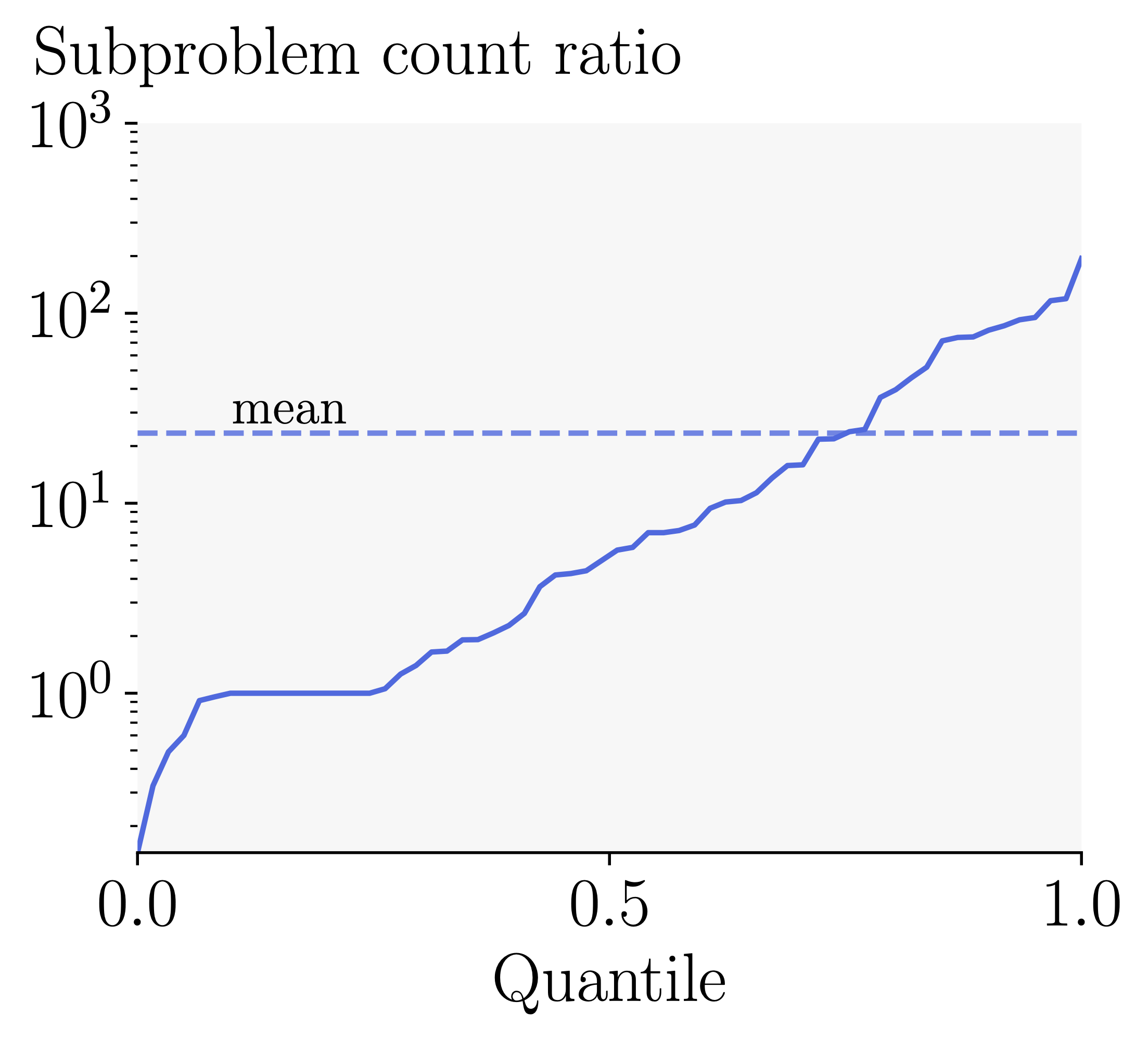
\(15\%\) of the texts produced by our strongest spoofing attacker are of high quality and manage to fool the watermark detector. Orthogonal to the problem of making this number higher, we ask: Are these spoofed texts really indistinguishable from genuinely watermarked texts? As we showed in “Discovering Clues of Spoofed LM Watermarks”, the answer is often no, as learning-based spoofers (both Stealing and Distillation) leave clues of spoofing in their outputs, and these can be used to flag such attempts. We repeat those experiments on a dataset of \(2000\) attempts to spoof SynthID-Text through stealing, evaluating our clue detector:
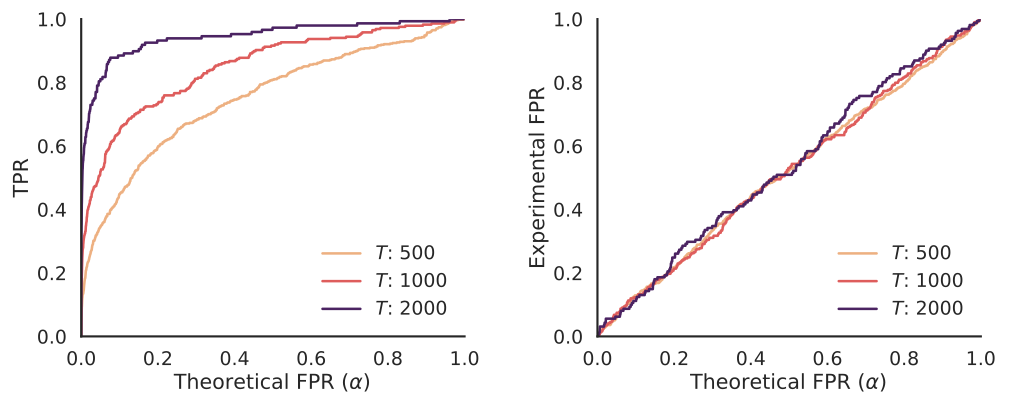
On the right, we see that our clue detector is properly calibrated, as the theoretical FPR (\(\alpha\)) matches the experimental FPR. On the left, we see that given total text length of \(T\), our clue detector has high power, similar to the results on SOTA schemes in the original paper. This implies an additional hurdle that attempts to improve spoofing attacks need to overcome to present a significant threat.
Summary: Stealing-based spoofers of SynthID-Text, despite limited success rate, leave detectable clues.
Future Work: Does the same conclusion hold for distillation-based spoofing? Can we design more elaborate spoofing attacks that would circumvent current clue detection, or overcome this issue entirely?
4. SynthID-Text is easy to scrub
Finally, we study the ability of attackers to remove (scrub) the watermark from watermarked texts via paraphrasing. Effective scrubbing techniques pose a threat to the usefulness of watermarks, as they allow the model to be used as if it were not watermarked. This was briefly studied in the SynthID-Text supplementary text (C.6), where the results (e.g., the watermark AUC reduced to \(0.7\) for texts of \(1000\) tokens) already suggest that scrubbing may be possible. However, this experiment lacks a text quality evaluation, and uses only the average-case AUC metric, which is a poor measure of watermark effectiveness in relevant scenarios. Further, it does not explore assisted scrubbing—as we show in “Watermark Stealing in Large Language Models”, vulnerability to stealing can often greatly boost the success rate of scrubbing attacks.
We fill these gaps by directly applying our stealing attacker to SynthID-Text in a hard practical scenario, measuring success as FNR*@1e-3: the ratio of scrubbing attempts that are good paraphrases (using the P-SP metric) and are treated as unwatermarked by the watermark detector at a realistic false positive rate of \(10^{-3}\).
Click to see boring experimental details
As in our Spoofing experiments above, we use Llama2-7B as the watermarked model, and the same corpus of watermarked responses as the attacker's training corpus. We use DIPPER-11B as the baseline paraphraser. To generate scrubbing targets we query the watermarked model using Dolly writing prompts, which results in texts of average length of $1000$ tokens, reduced on average to $900$ tokens after scrubbing. All other details are the same as in the Spoofing experiments above.The gray bars show the success rate of the baseline paraphraser, and the purple bars show the improvement when stealing is used to assist the scrubbing process:
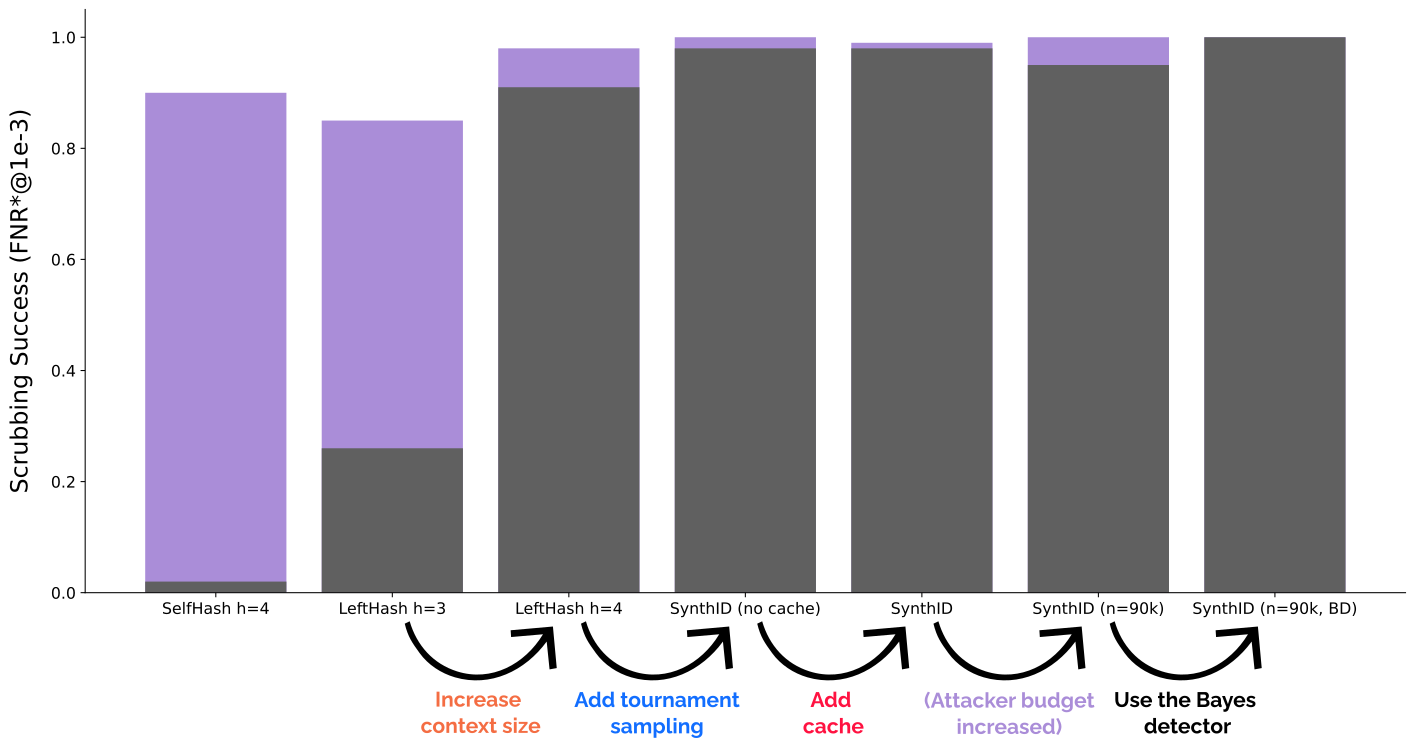
First two bars, copied from our paper, show that SOTA Red-Green watermarks are in this hard setting not easy to scrub using a baseline paraphraser, but this can be overcome by applying stealing as the first step (\(2\% \to 90\%\) and \(26\% \to 85\%\), respectively). Increasing context size, adding tournament sampling, and caching all lead to extremely high scrubbing success rates (above \(90\%\)), even without stealing, even when directly adding tournament sampling to LeftHash h=3 (not shown in the plot above). This means that even less powerful adversaries can easily scrub SynthID-Text from watermarked texts. The biggest loss in robustness comes from using \(h=4\), which is expected per the spoofing-scrubbing tradeoff. One way to somewhat mitigate this and raise the bar for the attackers (requiring larger budgets for successful scrubbing) is exemplified by SelfHash; combinations with SynthID-Text may be an interesting direction to explore in the future. While with these results it is hard to make conclusive statements about the effect of other novel components, tournament sampling seems to further decrease the robustness, suggesting that its \(g\) values are more sensitive to rewrites.
Summary: For naive adversaries only using off-the-shelf paraphrasers, SynthID-Text is easier to scrub compared to other SOTA schemes. This can further be boosted to nearly \(100\%\) by using black-box queries to first steal the watermark before scrubbing it.
Future Work: Can we better understand the effect of other components on scrubbing resistance? Can scrubbing robustness be improved without sacrificing watermark effectiveness and increasing spoofing risk? Would this hold under attempts to adapt prior scrubbing attacks to this scheme?
]]>
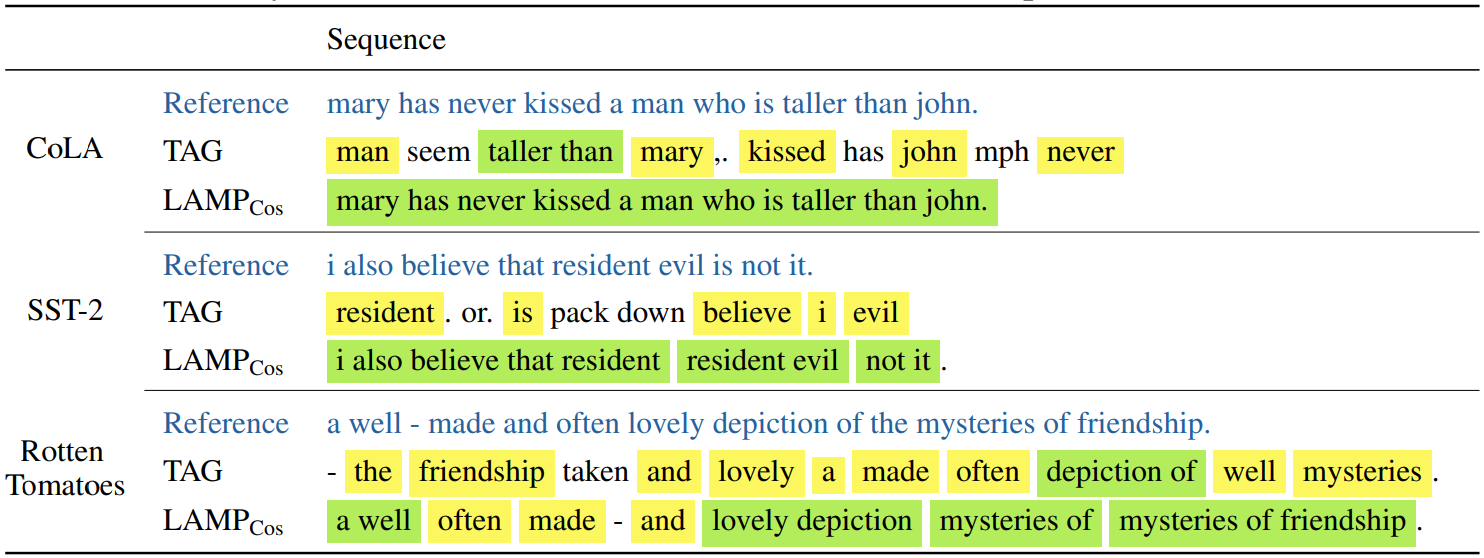 Here, yellow signifies a single correctly reconstructed word and green signifies a tuple of correctly recovered words. We see that LAMP recovers the word order drastically better and often is even able to reconstruct it perfectly. In addition, LAMP recovers more individual words. This confirms qualitatively the effectiveness of our attack.
Here, yellow signifies a single correctly reconstructed word and green signifies a tuple of correctly recovered words. We see that LAMP recovers the word order drastically better and often is even able to reconstruct it perfectly. In addition, LAMP recovers more individual words. This confirms qualitatively the effectiveness of our attack.