The Optimal Privacy Attack on Federated Learning
Mislav Balunović
April 20, 2022
Federated learning has become the most widely used approach to collaboratively train machine learning models without requiring training data to leave devices of the individual users. In this setting, clients compute updates on their own devices, send the updates to a central server which aggregates them and updates the global model. Because user data is not shared with the server or other users, this framework should, in principle, offer more privacy than simply uploading the data to a server. There have been several works which showed that data can in fact be reconstructed from the gradient updates sent to the server. In our work, we investigate what is the optimal attack for reconstructing data from gradients.
Privacy in federated learning
Goal of federated learning is to train a model $h_\theta$ through a collaborative procedure involving different clients, without data leaving individual client devices. Typically $h_\theta$ is a neural network with parameters $\theta$, classifying an input $x$ to a label $y$. We assume that pairs $(x, y)$ are coming from a distribution $\mathcal{D}$. In the standard federated learning setting, there are $n$ clients with loss functions $l_1, …, l_n$, who are trying to jointly solve the optimization problem and find parameters $\theta$ which minimize their average loss:
\[\begin{equation*} \min_{\theta} \frac{1}{n} \sum_{i=1}^n \mathbb{E}_{(x, y) \sim \mathcal{D}} \left[ l_i(h_\theta(x), y) \right]. \end{equation*}\]In a single training step, each client $i$ first computes $\nabla_{\theta} l_i(h_\theta(x_i), y_i)$ on a batch of data $(x_i, y_i)$, then sends these to the central server that performs a gradient descent step to obtain the new parameters $\theta’ = \theta - \frac{\alpha}{n} \sum_{i=1}^n \nabla_{\theta} l_i(h_\theta(x_i), y_i)$, where $\alpha$ is a learning rate. We will consider a scenario where each client reports, instead of the true gradient $\nabla_{\theta} l_i(h_\theta(x_i), y_i)$, a noisy gradient $g$ sampled from a distribution $p(g|x)$, which we call a defense mechanism. This setup is fairly general and captures common defenses such as DP-SGD. In this post, we are interested in the privacy issue of federated learning: can the input $x$ be recovered from gradient update $g$? More specifically, we are interested in analyzing the Bayes optimal attack and connecting it to the attacks from prior work.
Bayesian framework for gradient leakage
To measure how well can adversary reconstruct user data we introduce the notion of adversarial risk for gradient leakage, and then derive the Bayes optimal adversary that minimizes this risk. The adversary can only observe the gradient $g$ and tries to reconstruct the input $x$ that produced $g$. Formally, the adversary is a function $f: \mathbb{R}^k \rightarrow \mathcal{X}$ mapping gradients to inputs. Given some $(x, g)$ sampled from the joint distribution $p(x, g)$, the adversary outputs the reconstruction $f(g)$ and incurs loss $\mathcal{L}(x, f(g))$, which is a function $\mathcal{L}: \mathcal{X} \times \mathcal{X} \rightarrow \mathbb{R}$.
The loss measures whether the advesary was able to reconstruct the original data. Typically, we will consider a binary loss that evaluates to 0 if the adversary’s output is close to the original input, and 1 otherwise. If the adversary only wants to get to some $\delta$-neighbourhood of the input $x$ in the input space, an appropriate definition of the loss can be $\mathcal{L}(x, x’) := 1_{||x - x’||_2 > \delta}$. This definition is well suited for image data, where $\ell_2$ distance captures our perception of visual similarity. We can now define the risk $R(f)$ of the adversary $f$ as
\[\begin{equation} R(f) := \mathbb{E}_{x, g} \left[ \mathcal{L}(x, f(g)) \right] = \mathbb{E}_{x \sim p(x)} \mathbb{E}_{g \sim p(g|x)} \left[ \mathcal{L}(x, f(g)) \right]. \end{equation}\]We can then manipulate this expression and show that \(R(f) = 1 - \mathbb{E}_g \int_{B(f(g), \delta)} p(x|g) \,dx\). This allows us to work out what is the optimal adverasary $f$ which minimizes the adversarial risk $R(f)$:
\[\begin{align} f(g) &= \underset{x_0 \in \mathcal{X}}{\operatorname{argmax}} \int_{B(x_0, \delta)} p(x|g) \,dx \nonumber \\ &= \underset{x_0 \in \mathcal{X}}{\operatorname{argmax}} \int_{B(x_0, \delta)} \frac{p(g|x)p(x)}{p(g)} \nonumber \,dx \\ &= \underset{x_0 \in \mathcal{X}}{\operatorname{argmax}} \int_{B(x_0, \delta)} p(g|x)p(x) \,dx \nonumber \\ &= \underset{x_0 \in \mathcal{X}}{\operatorname{argmax}} \left[ \log \int_{B(x_0, \delta)} p(g|x)p(x) \,dx \right] \label{eq:optadv} %% &\geq \argmax_{x_0 \in \mathcal{X}} \int_{B(x_0, \delta)} \log p(g|x) + \log p(x) \,dx \label{eq:optadv} \end{align}\]While the above provides a formula for the optimal adversary in the form of an optimization problem, using this adversary for practical reconstruction is computationally difficult so we can approximate it by applying Jensen’s inequality \(\log C \int_{B(x_0, \delta)} p(g|x)p(x) \,dx \geq C \int_{B(x_0, \delta)} (\log p(g|x) + \log p(x)) \,dx.\)
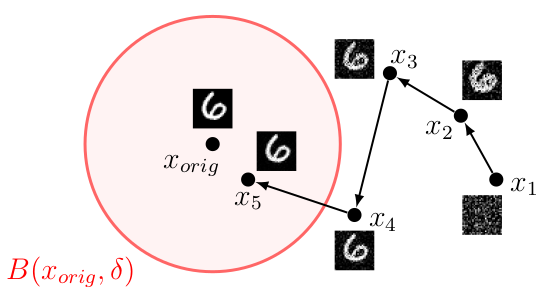
Gradient leakage attack. Bayes optimal adversary randomly initializes the image and then optimizes for the image which has highest likelihood of being close to the original image which produced the gradient.
We can then approximate the integral by Monte Carlo sampling and optimize the objective using gradient descent. As shown in the figure above, adversary can randomly initialize the input, and then optimize for the input which has highest likelihood of being close to the original input which produced the update gradient $g$. One interesting thing is that we can now recover attacks from prior work by using different priors $p(x)$ and conditional $p(g|x)$, meaning that attacks from prior work are different approximations of the Bayes optimal adversary. For example, DLG is recovered by using uniform prior and Gaussian conditional, another attack is recovered by using total variation prior and cosine conditional, while GradInversion uses combination of total variation and DeepInversion prior combined with Gaussian conditional.
Attacking existing defenses
In this experiment, we evaluate the three recently proposed defenses Soteria, ATS and PRECODE against strong gradient leakage attacks. While these defenses can protect privacy against weaker attackers (as shown in the respective papers), we show that they are not actually successful against strong attacks. Below we show our reconstructions for each defense, evaluated on CIFAR-10 dataset.

Reconstructions on defended networks. We attack models defended by Soteria, ATS and PRECODE using strong attacks. Our reconstructions are very close to the original images, showing that these defenses do not reliably protect privacy, especially early in training.
Each defense introduces a different $p(g|x)$ which we use to derive an approximation of Bayes optimal adversary. Our results indicate that these defenses do not reliably protect privacy under gradient leakage, especially in the early stages of the training. This suggests that creating effective defenses and strong evaluation methods remains a key challenge. We provide full description of these defenses and our attacks in our paper.
Comparing different attacks
In the next set of experiments we compare Bayes optimal attack with several other, non-optimal attacks. We consider several different defenses all of which produce different distributions $p(g|x)$. One defense adds Gaussian noise, another randomly prunes out some elements of the gradient and then adds Gaussian noise, and the third one adds Laplacian noise after pruning. We measure PSNR of the reconstructions, where higher value means that reconstruction is closer to the original image.
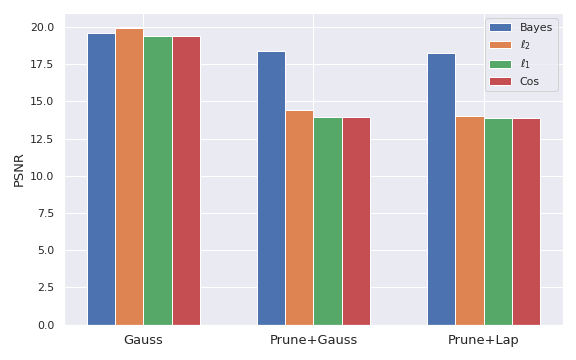
Bayes optimal attack compared to other attacks. We consider several different defenses with adding Gaussian or Laplacian noise or pruning and show that Bayes optimal attack is typically the best.
We observe that Bayes optimal adversary generally performs best, showing that the optimal attack needs to leverage structure of the probability distribution of the gradients induced by the defense. Note that, in the case of Gaussian defense, $\ell_2$ and Bayes attacks are equivalent up to a constant factor, and it is expected that they achieve a similar result. In all other cases, Bayes optimal adversary outperforms the other attacks. Overall, this experiment provides empirical support for our theory, confirming practical utility of the Bayes optimal adversary.
Summary
In this blog post we considered the problem of privacy in federated learning and investigated the Bayes optimal adversary which tries to reconstruct original data from the gradient updates. We derived form of this adversary and showed that attacks proposed in prior work are different approximations of this optimal adversary. Experimentally, we showed that existing defenses do not protect against strong attackers, and that deriving good defense remains an open challenge. Furthermore, we showed that Bayes optimal adversary is stronger than other attacks when it can exploit structure in probability distributions, confirming our theoretical results. For more details, please check out our ICLR 2022 paper.

