Reliability Guarantees on Private Data
Nikola Jovanović
November 7, 2022
In this post we present our ACM CCS 2022 publication, Private and Reliable Neural Network Inference, where we introduced Phoenix, a tool for NN inference that both protects client data privacy and enables important reliability guarantees.
We focus on the common ML as a service scenario, a two-party setting where a client offloads intensive computation (commonly NN inference) to the server. The client data is of sensitive nature in many of the applications (e.g., financial, judicial), which motivated work in the field of privacy-preserving NN inference, aiming to build methods that perform the computation without the server learning the client data. One of the most common techniques for this is fully-homomorphic encryption (FHE), which is rapidly becoming more practical.
Orthogonal to privacy, a long line of work focuses on enabling NN inference with reliability guarantees. For example, in a loan prediction setting, augmenting predictions with fairness guarantees is in the interest of both parties, as it increases trust in the system and may be essential to ensure regulatory compliance. Some of the latest works in this direction are LASSI and FARE, focusing on two aspects of the fairness problem. Another common example is robustness, where for example, a medical image analysis system should be able to prove to clients that the diagnosis is robust to naturally-occurring measurement errors (see e.g., our latest work SABR).
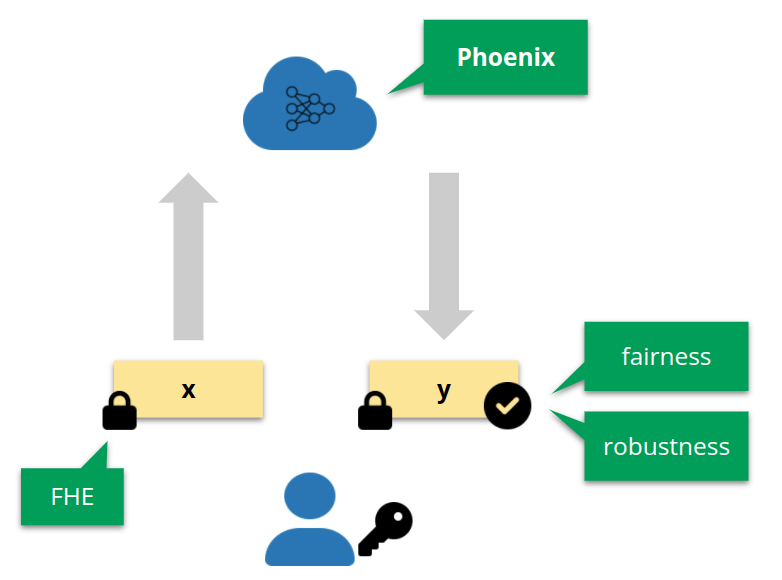
ML as a service. Phoenix achieves both client data privacy (via FHE) and fairness/robustness guarantees.
While the problems of privacy-preserving and reliable inference are both well-established, there was no prior attempt to consolidate the work in these two fields. Thus, service providers who offer reliability guarantees currently have no simple way to transition their service to a privacy-preserving setting, a requirement which is becoming increasingly relevant. This is the problem we address in Phoenix, proposing a system that supports both: client data privacy and reliability guarantees. To this end, we lift the key building blocks of randomized smoothing, a technique for augmenting predictions with reliability guarantees, to the popular RNS-CKKS FHE scheme. The key challenges that Phoenix overcomes stem from the missing native support for control flow and evaluation of non-polynomial functions in the FHE scheme.
We now recall randomized smoothing on a high level.
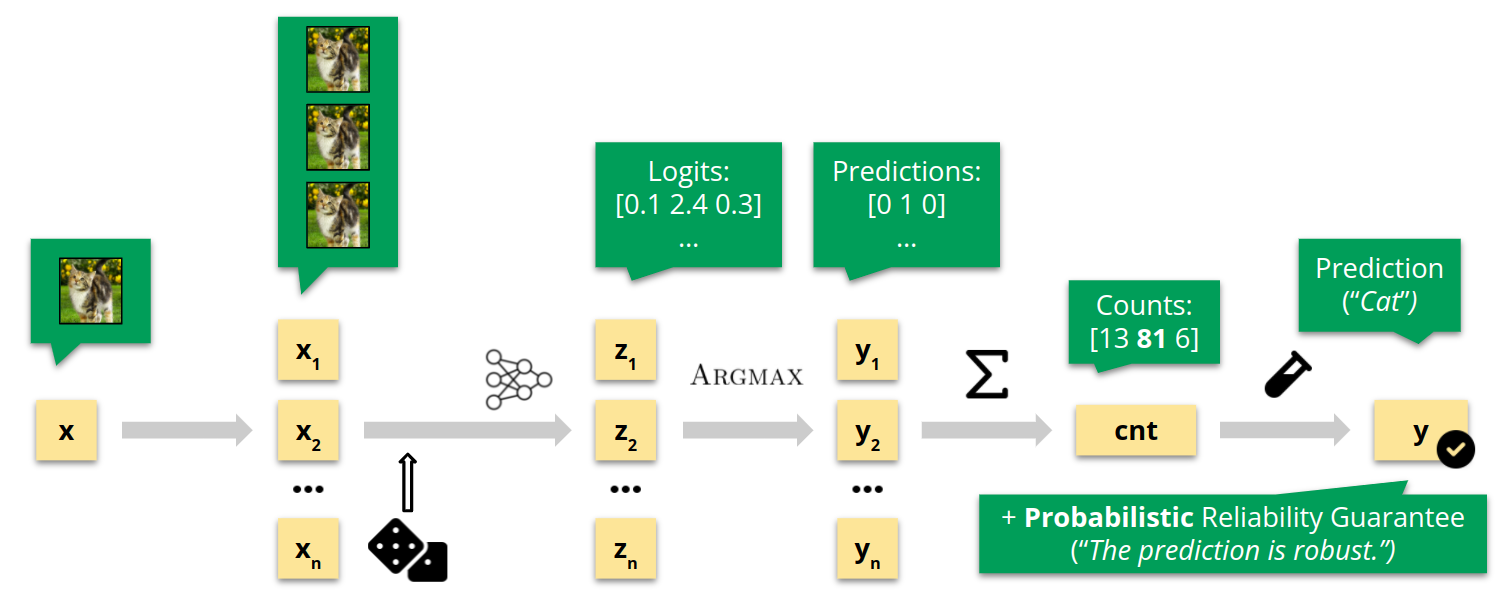
Randomized smoothing. A high-level overview of the procedure in the non-private setting.
As the service provider, we receive an input $x$ (in the illustration above, a cat image), and we aim to return a prediction $y$ (for some classification task) augmented with a reliability guarantee, for a property such as robustness. We duplicate the input $n$ times, add independently sampled Gaussian noise to each copy, and perform batched NN inference to obtain the logit vectors, i.e., unnormalized probabilities. Next, we apply the Argmax function to transform logits to predictions, and aggregate those predictions across $n$ samples to get the counts, indicating how many times each output class was predicted. Finally, we perform a statistical test on the counts, which, if successful, produces a probabilistic reliability guarantee, ensuring that the prediction $y$ is robust with known high probability.
The key question is how this procedure needs to change if we attempt to execute it while protecting client data privacy, i.e., if the data is encrypted using FHE by the client. The key steps are illustrated below.
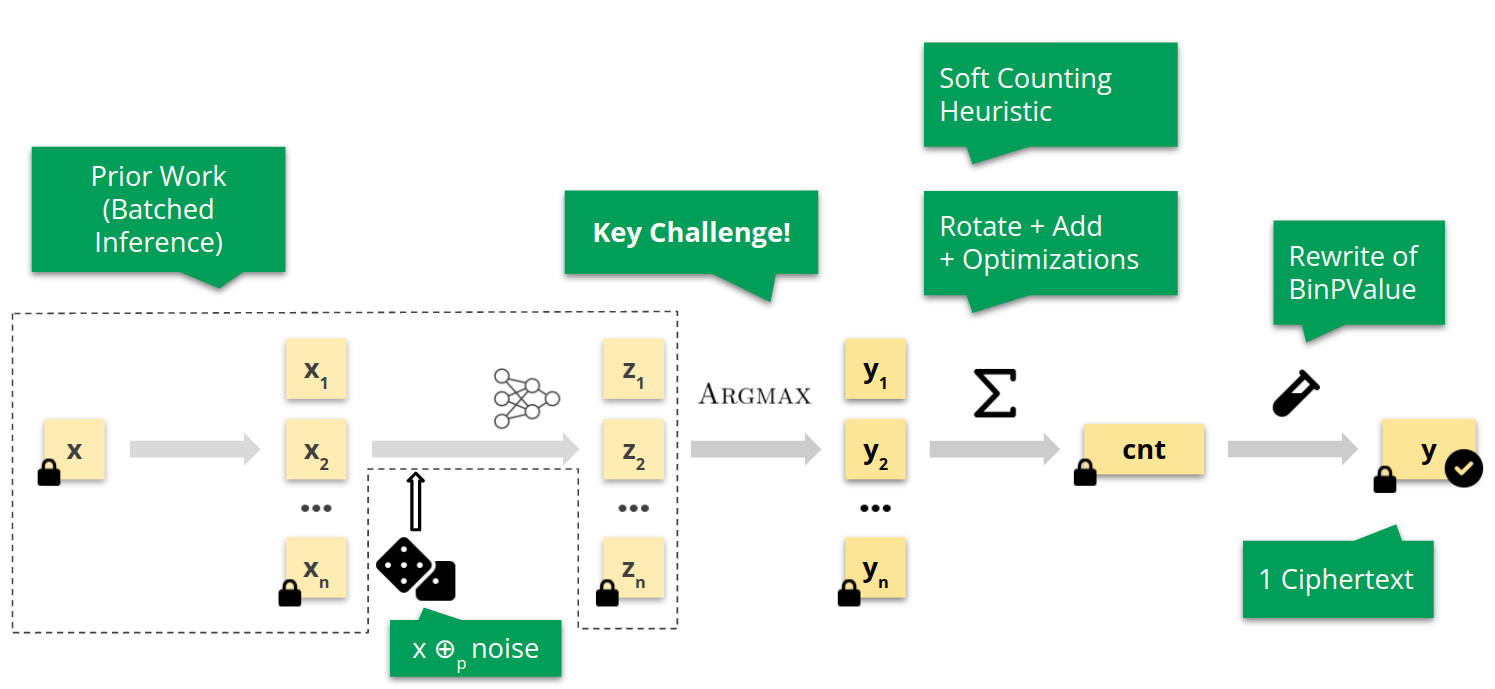
Overview of Phoenix. The main challenges in lifting randomized smoothing to FHE.
For the batched NN inference (dashed line) we directly utilize prior work, which offers efficient algorithms for the RNS-CKKS scheme. Further, the addition of noise is simple, as the noise can be directly added as a plaintext due to the homomorphic property. However, computing Argmax is a key challenge due to the difficulty of computing non-polynomial functions—we elaborate on this shortly. In the aggregation step we combine several methods from prior work with scheme-specific optimizations, and develop a novel heuristic for randomized smoothing, necessary to obtain a computationally feasible procedure. Finally, we perform a rewrite of the one-sided binomial test applied to counts to make it FHE-suitable. The output of Phoenix is a single ciphertext, which when decrypted with the secret key of the client, reveals both the prediction and the computed reliability guarantee. We next discuss the Argmax approximation in more detail, and refer to our paper for details regarding all other steps.
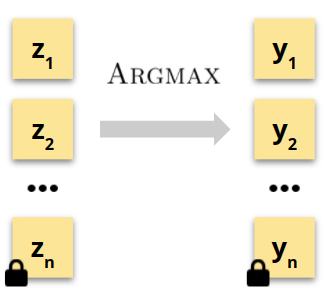 To efficiently approximate Argmax, we use the recent paper of Cheon et al. (ASIACRYPT ‘20), which propose SgnHE, a sign function approximation for FHE as a composition of low-degree polynomials, illustrated below.
Our approximate Argmax is built on several applications of SgnHE (see the paper for the full algorithm).
Most importantly, in our case it is crucial to have guarantees on the approximation quality of SgnHE—otherwise, the randomized smoothing reliability guarantee returned to the clients may in some cases be invalid, fundamentally compromising the protocol.
To efficiently approximate Argmax, we use the recent paper of Cheon et al. (ASIACRYPT ‘20), which propose SgnHE, a sign function approximation for FHE as a composition of low-degree polynomials, illustrated below.
Our approximate Argmax is built on several applications of SgnHE (see the paper for the full algorithm).
Most importantly, in our case it is crucial to have guarantees on the approximation quality of SgnHE—otherwise, the randomized smoothing reliability guarantee returned to the clients may in some cases be invalid, fundamentally compromising the protocol.
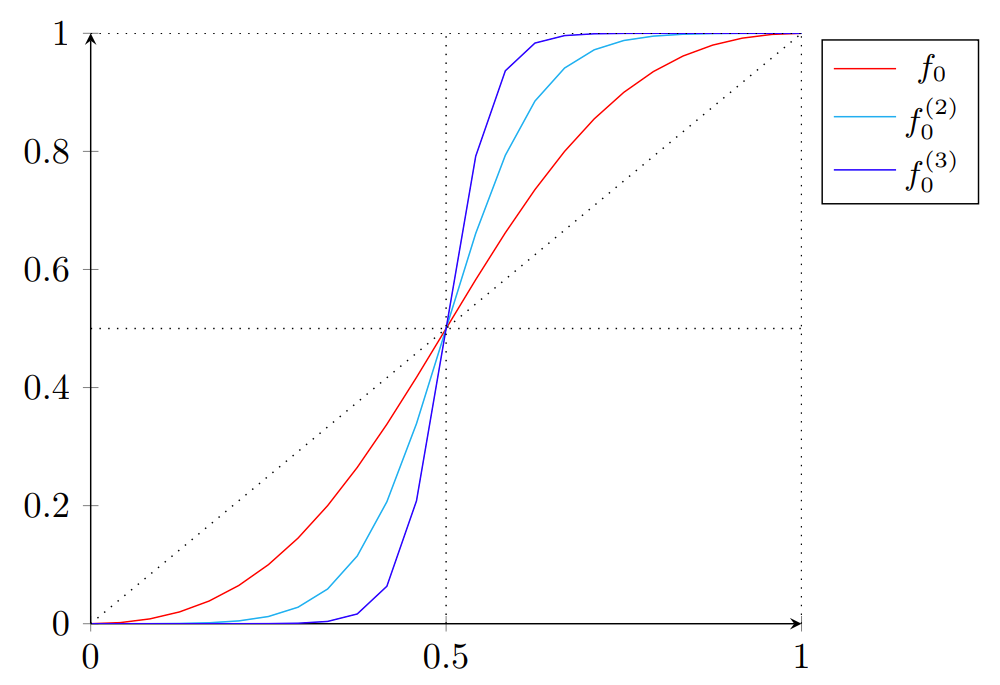
Sign function approximation. Repeated applications of the polynomial $f_0$ increase approximation quality.
The SgnHE function is parametrized such that for desired parameters $a,b \in \mathbb{R}$, we can obtain an $(a,b)$-close approximation, meaning that for inputs $x \in [a, 1]$ the output is guaranteed to be in $[1 - 2^{-b}, 1]$ (similarly for the negative case). However, as the server is unable to directly observe the intermediate values due to encryption, it is hard to ensure the above precondition is satisfied for logit values which are the input to the Argmax, and the first of the sign function applications it utilizes.
To overcome this we impose two conditions on the logit vectors, constraining the range and differences of their values, allowing us to appropriately rescale them and reason about the approximation quality. As we can not prove for an arbitrary NN that such conditions on logits will always hold (e.g., be in some range), we use confidence intervals and a finite sample to upper bound the condition violation probability. When reporting the guarantee to the client, the computed probability (approximation error) is added to the usual error probability of randomized smoothing as the probabilistic procedure (algorithmic error). The resulting value represents the total error probability of our guarantee, maintaining the behavior of the non-private case.
In our extensive experiments across multiple scenarios we observe values for the total error probability of around 1%, confirming that our procedure leads to viable high-probability guarantees. We further observe non-restrictive latencies and communication cost and high consistency, i.e., the results obtained with the FHE version of randomized smoothing are in almost 100% of the cases identical to those of the non-private baseline, confirming that transitioning a service to FHE using Phoenix does not sacrifice the key metrics. Our Microsoft SEAL implementation is publicly available on GitHub.
We believe Phoenix is an important first step towards merging the worlds of reliable and privacy-preserving machine learning. For more details of the Argmax approximation, omitted parts of the protocol, as well as detailed experimental results including microbenchmarks, please refer to our paper.

