Encoding Sensitive Data with Guarantees
Mislav Balunović
April 20, 2022
As machine learning is being increasingly used in scenarios that affect humans, such as credit scoring or crime risk assessment, it has become clear that these predictive models often discriminate and can be unfair. It is thus increasingly important to design methods that help models make fair decisions, either by pre-processing the input data, in-processing the model or post-processing the predictions. In our work, we propose a new pre-processing approach to encode existing data into new, unbiased representations that have high utility, but do not allow for reconstructing sensitive attributes such as race or gender. Our approach, named Fair Normalizing Flows (FNF) is based on learning a bijective encoder for each group (where groups are determined based on the sensitive attribute). Using bijective encoders enables us to obtain guarantees on maximum accuracy that any adversary can have when predicting the sensitive attribute.
Fair representations
Consider a case of a company with several teams that would like to build ML models for different products using the same data. One option would be for each team to train their own model and enforce fairness of the model by themselves. However, the teams might not have the same definition of fairness or they might even lack expertise to train fair models. Fair representation learning is a data pre-processing technique that transforms data into a new representation such that any classifier trained on top of this representation is fair. Using representation learning enables us to pre-process data only once, and then give processed data to each team so that they can train their own model on this new data, while knowing that the model is fair, according to a single, pre-defined fairness definition. The key question here is how to ensure that sensitive attributes cannot be recovered from the learned representations. Typically, prior work has checked that this is the case by jointly learning representations and an auxiliary adversarial model which is trying to predict the sensitive attribute from the representations. However, while these representations protect against adversaries considered during training, several recent papers have shown that stronger adversaries can often in fact still recover the sensitive attributes. Our work tackles this issue by proposing non-adversarial fair representation learning approach based on normalizing flows which can in certain cases guarantee that no adversary can reconstruct the sensitive attributes.
Motivation
To motivate our fair representation learning approach, we introduce a small example of a population consisting of a mixture of 4 Gaussians. Consider a distribution of samples $x = (x_1, x_2)$ divided into two groups, shown as blue and orange in the figure below, with color and shape denoting sensitive attribute and label, respectively.
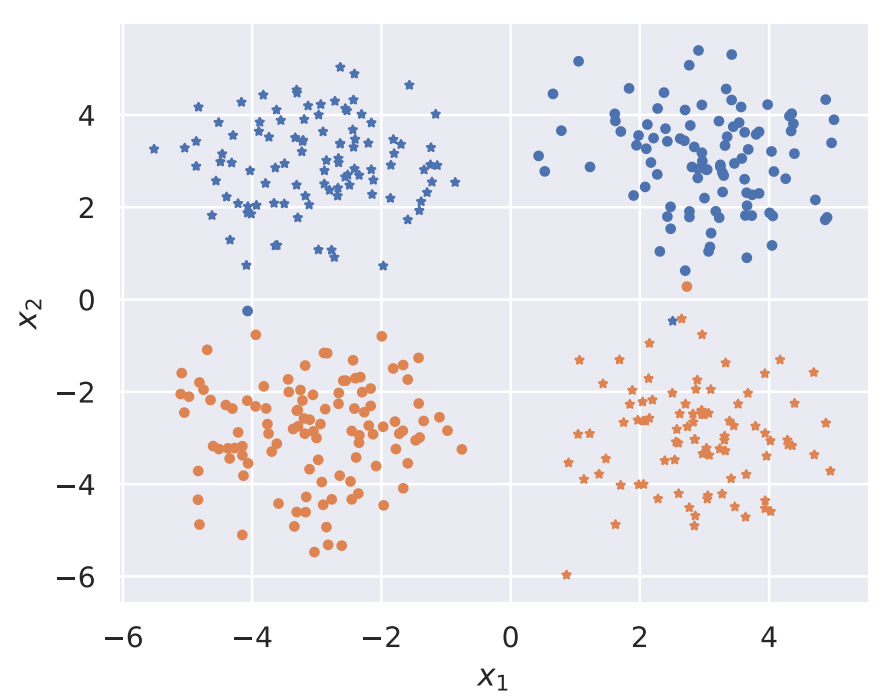
Example of a population. Sensitive attribute is determined using color and shape denotes the label.
The first group with a sensitive attribute $a = 0$ has a distribution $(x_1, x_2) \sim p_0$, where $p_0$ is a mixture of two Gaussians at the top half. The second group with a sensitive attribute $a = 1$ has a distribution $(x_1, x_2) \sim p_1$, where $p_1$ is a mixture of two Gaussians at the bottom half. The label of a point $(x_1, x_2)$ is defined by $y = 1$ if $x_1$ and $x_2$ have the same sign, and $y = 0$ otherwise. Our goal is to learn a data representation $z = f(x, a)$ such that it is impossible to recover $a$ from $z$, but still possible to predict target $y$ from $z$. Note that such a representation exists for our task: simply setting $z = f(x, a) = (-1)^ax$ makes it impossible to predict whether a particular $z$ corresponds to $a = 0$ or $a = 1$, while still allowing us to train a classifier $h$ with essentially perfect accuracy (e.g. $h(z) = 1$ if and only if $z_1 > 0$). This example also motivates our general approach: can we somehow map distributions corresponding to the two groups in the population to new distributions which are guaranteed to be difficult to distinguish?
Fair Normalizing Flows
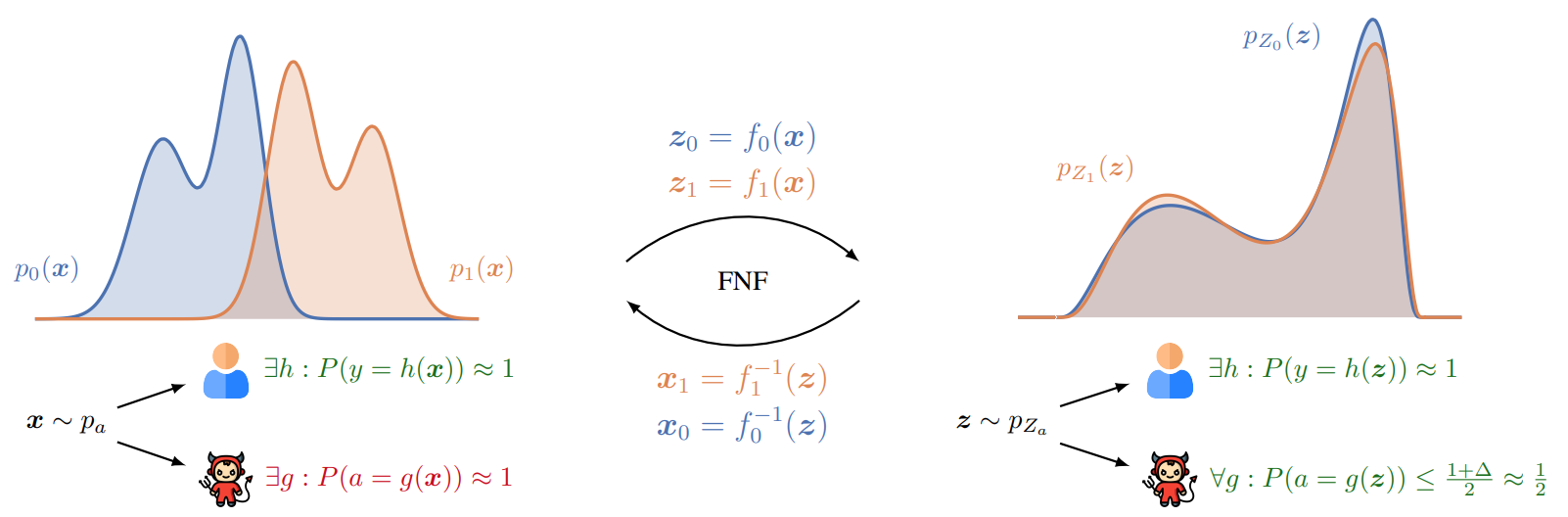
Overview of FNF. The key idea is to transform distributions corresponding to different groups using bijective encoders. After training, two distributions are aligned, and adversary cannot reconstruct sensitive attribute $a$ from the latent representation $z$.
As shown in the figure above, original features are useful for solving some downstream prediction task: we can train a classifier $h$ which predicts task label from the original features $x$ with reasonable accuracy. However, at the same time, an adversary $g$ can recover sensitive attribute from $x$, and use it to potentially discriminate in a downstream task. Motivated by the previous example, our goal is now to learn a function $f$ which transforms a pair of features and sensitive attribute $(x, a)$ into a new representation $z$ from which it is difficult to recover the sensitive attribute $a$. As in the previous example, we are going to encode both distributions corresponding to $a = 0$ and $a = 1$ using a bijective transformation. Our approach learns two bijective functions $f_0(x)$ and $f_1(x)$, and we denote the transformation as $f(x, a) = f_a(x)$.
One important quantity which we are interested in computing is statistical distance which measures how well can adversary distinguish between the distributions corresponding to the two groups in the population. Importantly, Madras et al. have shown that bounding statistical distance also bounds other fairness measures such as demographic parity or equalized odds. The statistical distance between the two encoded distributions, denoted as \(\mathcal{Z}_0\) and \(\mathcal{Z}_1\) is defined as:
\[\begin{equation} \Delta(p_{Z_0}, p_{Z_1}) \triangleq \sup_{\mu \in \mathcal{B}} \lvert \mathbb{E}_{z \sim \mathcal{Z}_0} [\mu(z)] - \mathbb{E}_{z \sim \mathcal{Z}_1} [\mu(z)] \rvert, \end{equation}\]where \(\mu\colon \mathbb{R}^d \rightarrow \{0, 1\}\) is a function from the set of all binary classifiers $\mathcal{B}$, trying to discriminate between $\mathcal{Z}_0$ and $\mathcal{Z}_1$. We can show that supremum is attained for $\mu^*$ which, for some $z$, evaluates to \(1\) if and only if \(p_{Z_0}(z) \leq p_{Z_1}(z)\). This shows that for computing statistical distance we need to know how to evaluate probability densities in the latent space, which is difficult for standard neural architectures because any $z$ can correspond to the several different inputs $x$. However, our approach uses bijective transformation for an encoder, and it is easy to compute the latent probability density using the change of variables formula:
\[\begin{equation} \log p_{Z_a}(z) = \log p_a(f^{-1}_a(z)) + \log \left | \det \frac{\partial f^{-1}_a(z)}{\partial z} \right | \end{equation}\]We train the two encoders $f_0$ and $f_1$ to minimize the statistical distance $\Delta(p_{Z_0}, p_{Z_1})$, while at the same time we can also train an auxiliary classifier which helps learned representations to be informative for downstream prediction tasks. One issue with training this way is that statistical distance is non-differentiable, as optimal adversary $\mu^*$ makes discrete thresholding decision, so we instead train by minimizing a loss which is a smooth approximation of the statistical distance. After training is finished, we can evaluate statistical distance exactly, without any approximation. Our guarantees assume that we know input distributions $p_0$ and $p_1$, which we most often have to approximate in practice. You can find full details of how our guarantees change when input distributions are estimated in our paper.
Experimental evaluation
We evaluated FNF on several standard datasets from the fairness literature. For each dataset, we take one of the features to be a sensitive attribute (e.g. race), and we train a model which balances between accuracy, measuring how well can it predict a task label, and fairness, measuring how well can it debias the learned representations from the sensitive attributes.
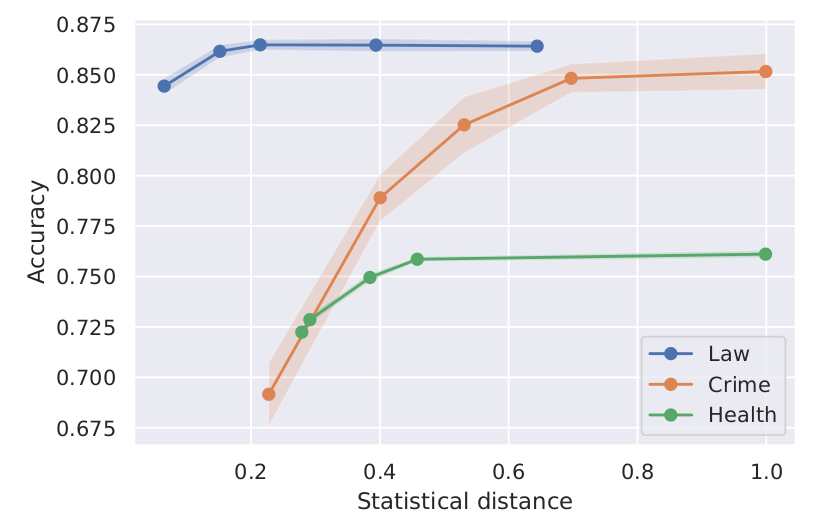
Tradeoff between accuracy and fairness with FNF. For each datasets we measure classification accuracy and statistical distance, and show that FNF achieves favorable tradeoff between these quantities..
The above figure shows results on Law School, Crime and Health Heritage Prize datasets, with each point representing a single model with different fairness-accuracy tradeoff. As a fairness metric, we measure statistical distance introduced earlier. We can observe that for all datasets FNF can effectively balance fairness and accuracy. In general, drop in accuracy is steeper for datasets where the task label is more correlated with the sensitive attribute. We provide more experimental results in our paper, including experiments with discrete datasets and comparison with prior work.
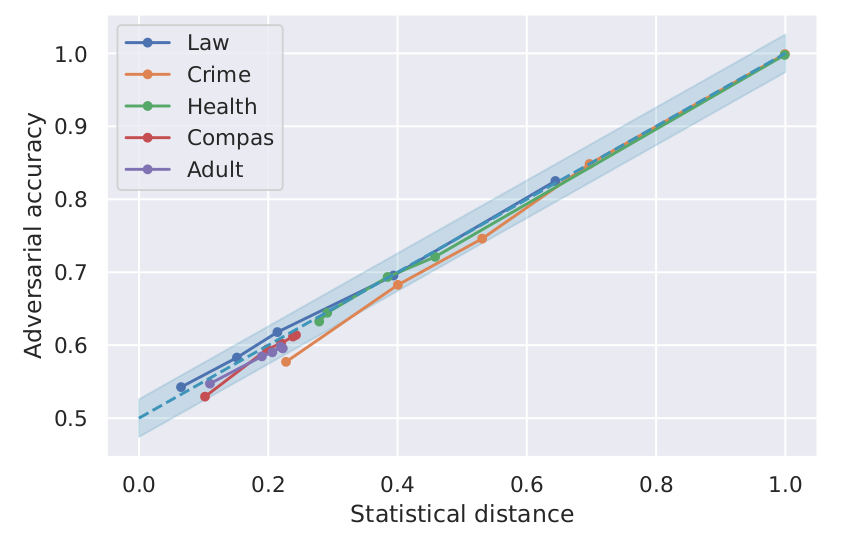
Bounding adversarial accuracy. We show that FNF can reliably bound maximum accuracy that any adversary can have when predicting sensitive attribute from the encoded representations.
As mentioned earlier, FNF provides provable upper bound on the maximum accuracy of the adversary trying to recover the sensitive attribute, for the estimated probability densities of the input distribution. We show our upper bound on the adversarial accuracy computed from the statistical distance using the estimated densities (diagonal dashed line), together with adversarial accuracies obtained by training an adversary, a multilayer perceptron (MLP) with two hidden layers of 50 neurons, for each model from the figure. We can observe that FNF can successfully bound accuracy of the strong adversaries, even though the guarantees were computed on the estimated distributions. In our paper, we also experiment with using FNF for other tasks such as algorithmic recourse and transfer learning.
Summary
In this blog post, we introduced Fair Normalizing Flows (FNF), a new method for learning representations ensuring that no adversary can predict sensitive attributes at the cost of a small decrease in accuracy. Our key idea was to use an encoder based on normalizing flows which allows computing the exact likelihood in the latent space, given an estimate of the input density. Our experimental evaluation on several datasets showed that FNF effectively enforces fairness without significantly sacrificing utility, while simultaneously allowing interpretation of the representations and transferring to unseen tasks. For more details please see our ICLR 2022 paper.

